Judges as Data curators cut Post-training Time to Half
ServiceNow x Collinear
tl;dr: Collinear correctness curators remove about 50% of the samples from Numina-math and match the SOTA performance with a 12B model. Curated dataset and post-trained models are publicly available.
Post-training is the key to unlocking the full potential of AI models. A key ingredient of post-training is the data, whether that is for continual pre-training (CPT), supervised fine-tuning (SFT), or for reinforcement fine-tuning (RFT). Models are what they eat, which means you cannot expect a frontier model if you are feeding poor-quality data. Curators — small specialized models that select the right data to train on — have the potential to massively improve training efficiency while maintaining or even improving state-of-the-art model performance.
This creates a powerful AI improvement flywheel: better data curation leads to better models, which can then be used to create even more sophisticated curators, continuing the cycle of improvement while dramatically reducing computational requirements.
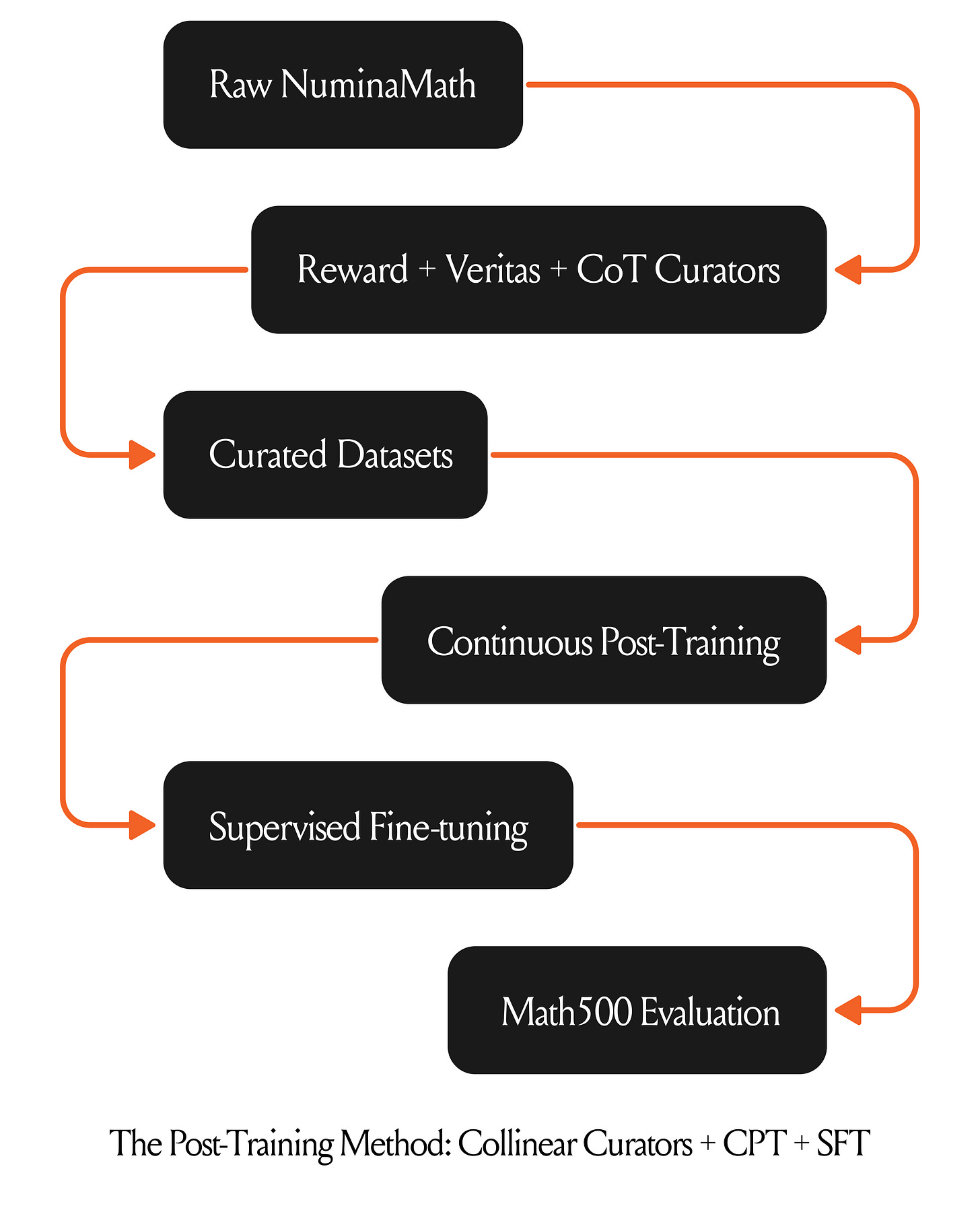
In collaboration with ServiceNow, we’ve been building curators for post-training frontier models in the range of 12B-23B to match the performance of models in the range of 32B-70B. This blog presents results on using Collinear math correctness curators used by ServiceNow for CPT of Mistral-NeMO-12B. We also show similar gains with SFT on a Phi-3.5B-instruct model using their curated data. The curated datasets and the post-trained models are now open-sourced and available on Hugging Face.
Enterprises with a GenAI strategy need to generate millions of synthetic examples each year for expanding and improving their core AI capabilities. In our work with ServiceNow, our goal was to curate high-quality math data with a focus on a low false positive rate (FPR) as the metric. This means that it is okay to filter out good examples as bad (FN) but it is NOT okay to let bad examples pass through (FP). We developed three math curators — a reward model that scores each data sample with an aggregated reward, a binary curator that classifies each data sample as good or bad, and a reasoning curator that rates each sample. We ensemble these curators to leverage their strengths for maintaining overall low FPR and high specificity.
We curated a dataset based on ServiceNow-AI/R1-Distill-SFT with 840K samples across school grade and competitive math challenges.
Math curators
Reward Model: We trained a lightweight ~450M smol model that takes as input the mathematical problem and solution and gives a continuous reward as the output. Built on high-quality curated open-source mathematical preference datasets of approximately ~350K size, the reward model is trained as an ORM (Outcome-supervised reward models). Beyond just correctness, it also implicitly assesses the quality of Chain-of-Thought (CoT) reasoning, ensuring more reliable mathematical evaluation.
Veritas: We also trained ~3.5B model on approximately 200K math solutions blending ServiceNow's synthetic generations with open-source SFT/preference datasets. The input format is similar to that of the Reward Model that we trained. Given a problem, a ground truth answer and generated solution(including the reasoning chain), the model outputs 1 or 0, based on the final answer's correctness. Similar to the reward model curator, the Veritas curator also implicitly checks the steps in the generated answer for correctness.
CoT curator: We fine-tuned a ~1B Math model to rigorously assess the quality of reasoning in step-by-step Chain-of-Thought (CoT) reasoning. Our approach involved augmenting OpenAI’s PRM800K (a process supervision dataset) with a strong emphasis on evaluating the correctness of each intermediate step in mathematical problem-solving. The resulting model demonstrated high precision in identifying incorrect responses (True Negatives).
Each individual model in our ensemble demonstrated strengths and weaknesses when evaluated in isolation. The Veritas-Phi model exhibited a low True Negative (TN) rate, meaning it classified very few examples as incorrect, but it was highly precise in identifying correct responses (high True Positive, TP). On the other hand, Qwen was an aggressive filter—it enforced strict correctness criteria, leading to a high TN rate and minimal False Positives (FP), but at the cost of filtering out too many correct responses (low TP), which negatively impacted downstream performance. The Reward Model (RM) was more balanced, maintaining a moderate False Negative (FN) rate while serving as an effective first-stage filter.
To leverage these strengths, we designed two ensemble configurations Collinear Curator 1(C1) and Collinear Curator 2(C2) , incorporating Veritas, RM and CoT curator predictions ensuring a balance between precision and recall. By ensembling these curators, we achieved a more refined selection process that maintains high specificity while mitigating the weaknesses of individual models.
Curated Dataset
The curated dataset is publicly available at Collinear-ai/R1-Distill-NuminaMath-Curation. This dataset consists of the NuminaMath samples from the ServiceNow-AI/R1-Distill-SFT dataset and has features problem, solution, source, R1-Distill-Qwen-32B, R1-Distill-Qwen-32B-messages, and correctness.
The problem, solution and source features are from the NuminaMath dataset and correspond to the problem statement, ground truth solution and problem source.
The R1-Distill-Qwen-32B feature contains the responses generated in response to the problem by the Qwen 32B model in the ServiceNow-AI/R1-Distill-SFT dataset, and the R1-Distill-Qwen-32B-messages feature is the response with chat formatting.
The correctness feature contains the judgments on correctness of the generated response by Collinear curators C1 and C2 as a json object where the values corresponding to the keys ‘C1’ and ‘C2’ are the curator predictions as to the correctness of the response.
Results
For evaluation, we used Math500 to benchmark the performance of models trained on the curated dataset.
CPT+ SFT Results
In this experiment, we achieved the final aligned model through a two-step alignment strategy designed to optimize performance on mathematical tasks. The process involved the following phases:
Phase 1: Continual Pre-training (CPT)
We performed continual pre training on the mistralai/Mistral-Nemo-Instruct-2407 model using the Collinear-curated Numina-Math dataset. This phase aimed to enhance the model's understanding of mathematical concepts, LaTeX symbols, and domain-specific token patterns.Phase 2: Supervised Fine-Tuning (SFT)
The model resulting from Phase 1 was further fine-tuned using the bespokelabs/Bespoke-Stratos-17k dataset. This step focused on aligning the model's outputs with task-specific instructions and improving its ability to generate accurate and contextually appropriate responses.
Empirical evidence showed that performing CPT before SFT led to a 30%+ improvement in accuracy on downstream mathematical tasks. The rationale behind this approach is rooted in the unique nature of mathematical and LaTeX symbols, which differ significantly from the conversational and general-domain data the base model was originally trained on. By first teaching the model to recognize and predict these specialized tokens (via CPT) and then fine-tuning it for task-specific performance (via SFT), we observed a substantial boost in its mathematical reasoning capabilities
The final fine-tuned model was evaluated on the MATH500 dataset, and its performance is depicted in Fig. 1. The control curated split is a random set from the unfiltered dataset of the same size as the respective curator split to establish and visualise the difference in performance. As shown, the model trained with the Collinear curated data achieved the same downstream accuracy as the model trained on the full unfiltered dataset, while utilizing less than 50% of the total dataset size i.e., ~2x speedup(measured in terms of processed tokens rather than dataset size). This demonstrates the high-quality curation provided by the Collinear curators, highlighting the effectiveness of carefully curated data in improving model performance.
SFT Results
As part of an additional study, we also fine-tuned (SFT) the microsoft/Phi-3.5-mini-instruct model on the Collinear curated numina-math datasets, and the results are presented in Fig. 2. The data clearly shows that the model trained with Collinear curated datasets performed at par with, or even surpassed, the model trained on the unfiltered dataset, despite using significantly less data. Additionally, this approach resulted in a performance speedup of approximately 1.8x, highlighting both the effectiveness and the efficiency of the Collinear curated datasets.